Angles in Standard Position and the Reference Angle
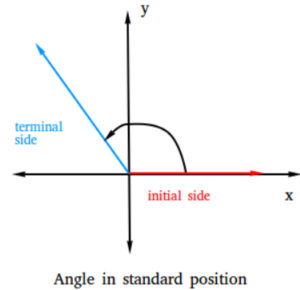
In its most basic form, trigonometry can be thought of as the relationship between an angle measure, either in degrees or radians, and the ratio of sides relative to the angle. It is important to understand trigonometric terminology. We have to be talking the same language.
We will explore the meaning of angles in standard position and define reference angles. Examples of sketches and how to determine the reference angle will be given.
Why is a Reference Angle so important?
Reference angles will assist us immensely in determining sine, cosine, and tangent ratios in any one of the four quadrants.
The following visual aid may also be useful.
https://mathbitsnotebook.com/Algebra2/TrigConcepts/TCStandardPosition.html
What is the next lesson?
Once the groundwork has been laid for understanding angles in standard position and reference angle, we move on to special triangle ratios. Working with these special ratios is crucial for Math 30-1.
